Crosswinds during takeoff and landing can be no big deal or a very big deal, depending on your adherence to procedure, application of sound technique, and the aircraft's design. Design? The published limitation or demonstrated value may not be what it claims to be. See Crosswind Landing for an example and explanation.
— James Albright
Getting a little cross with the winds
The official line was preached on day one and over again to those about to receive the big boot out the door: undergraduate pilot training was tough. Not everyone could cut the mustard and it didn’t matter how many civilian hours you had or how smart you were. Not everyone had what it takes and those who didn’t were shown the door with no hard feelings. Your official Air Force records would not reflect any hint of the negative experience and you would be sent on to other, very rewarding careers.
Right. It may have been true, but as our class started hemorrhaging officers — young men who got the taste of what it would be like to live in that rarified existence but would be further denied — we who survived felt even more pressure to continue surviving.
The first test was solo. In the T-37 you sat side-by-side and your instructor watched your every move from the right seat. Sitting on an ejection seat wrapped in nomex from head to toe, head encased in a plastic shell and oxygen mask; it would seem like an unlikely place to get to know somebody well enough to make such a career-altering decision. But it was easier than it might seem. At the end of that oxygen mask was a microphone connected to a “hot mike” interphone. You heard every sound emanating from the other pilot: every word, every gasp, every grunt. Even in March, the Arizona desert was hot and both pilots sat under a glass canopy like ants under a ten-year old’s magnifying glass. You got to know the other pilot’s scent. The cockpits reeked of sweat. You knew if the other pilot was under duress, you could sense exasperation as if it were a tangible fragrance in the oxygen-enriched air.
We longed for the day our instructors would hop out, entrusting us with the 6,000 pounds of metal, jet engines, glass, Jet-A fuel, explosive squibs, and all that other stuff that went with it. For me the day came exactly one month after my first ride in the jet. In our flight of thirty-nine officers, about ten of us soloed on the same day, followed by more and more as the week went on. There was no badge of merit, no added chevron, no outward sign given to those who made this first hurdle to announce elevation from mortal status. But you could tell.
Pre-solo, we inched down the halls to the flight room, tentative kittens, anxiously looking to the scheduling board for our next assignments and hoping to avoid the next catastrophe; Don’t let me wash out.
Post solo, we strolled — no, we swaggered — up and down the halls, blood-hungry predators, daring the entire Military Industrial Complex to throw the next challenge our way. After the initial solo, more challenges would come and soon it was up to us to check off items in our grade books along the road to getting our wings. “I’m going up today to perfect the transition from the Split-S to barrel roll,” we would say to anyone who cared to listen, “I think I can build enough energy with one roll to go right into a loop.” Between students we would brag, “I think I can do that Split-S inverted.”
As the next week turned into the week after that, our ranks were getting thinner. As the last of our solo washouts was out the door, the atmosphere between instructors and students forever changed. There was a new level of respect, I suppose. But with that respect came higher expectations.
I was in the pattern on a windy day and made an uneventful landing, albeit with a handful of aileron and rudder to keep the airplane off the Arizona desert either side of the runway. I walked into the flight room to an inquisition from my instructor, his boss, and his boss’s boss.
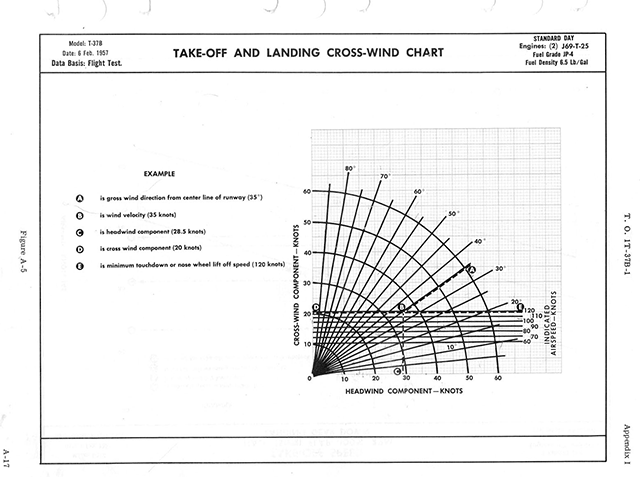
“Lieutenant,” the first lieutenant instructor began, “what is the dry runway crosswind limitation of the T-37B?”
“Seventeen point five knots,” I spat out while assuming the position of attention, “sir.”
“Why does that limit exist,” the captain standing to his right asked.
“The aircraft cannot maintain adequate ground control,” I answered, “after aerodynamic effectiveness is lost on the rudder with a crosswind above that speed, sir.”
“And what was the crosswind,” the major standing on everyone’s right asked, “when you landed thirty minutes ago?”
“Seventeen knots,” I ad-libbed, “sir.”
“Did you look that up?” my instructor asked.
“Ah,” I stammered, “no sir.”
I was given the next day off the flying schedule to consider my sins. The tower called the winds 260 at 25 when I first showed up in the pattern and there were three other Tweets doing the same thing I had planned, touch-and-go after touch-and-go until time or fuel was up. By the time I had two touch-and-go’s under my belt the pattern was empty but I didn’t have the gas for another, so I called one last time, “Gear down, full stop.”
“Cleared to land,” the tower said, “winds are 240 at 25.”
I landed.
The next day, looking at the chart I should have looked at the day prior, my transgressions became clear. Runway 30 has a magnetic heading of 300 degrees. When the winds were called 260 at 25, there was a forty degree difference and according to the chart I had a 16 knot crosswind, perfectly okay. When the winds changed to 240 degrees, the crosswind became 22 knots. Not good.
I placed a large tape marker on the crosswind chart in my checklist and moved on. There had to be an easier way, I knew. It was, after all, simple trigonometry. I knew the sine of 30 was half and the sine of 60 was the square root of three divided by two. But that wasn’t much help 60 seconds prior to landing breathing oxygen from a mask, sitting on an ejection seat, falling earthward at 1,500 feet per minute.
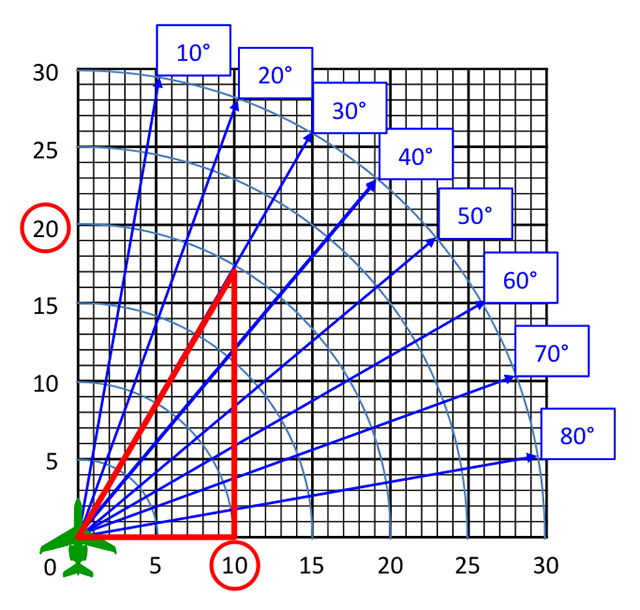
I decided to start with what I knew; the sine of 30 is half the value of the hypotenuse. Even the crosswind chart bore this out.
I drew a triangle and thought for a bit. A thirty degree right triangle has an opposite angle of 60 degrees. The opposite side would be equal to the sine of 30, or 0.5 times the hypotenuse. So the hypotenuse represents the wind, say 20 knots. With a 30 degree wind angle the crosswind is equal to half the wind, or 10 knots. This was basic trigonometry but hardly intuitive. Trigonometry worked, but I needed something I could explain without a book of tables. New sheet of paper. . .
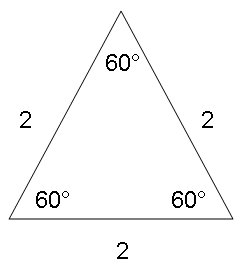
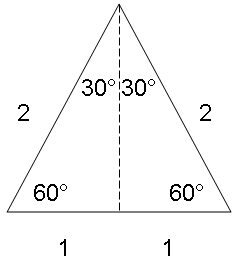
An equilateral triangle has three equal sides. If one side was equal to 2, all sides were equal to 2. Each angle would be equal to 60, because some theoretician discovered the sum of all angles has to equal 180 and that divided by three equal angles is 60. But that wasn’t helping my 30 degree rule at all.
Ah, but what if we cut one of those angles in half? That would also cut the opposite leg in half and give me my one-half solution.
Now, without that book of tables, I could prove the crosswind was equal to half the wind with a thirty degree angle:

A thirty degree crosswind is equal to one-half the full wind factor.
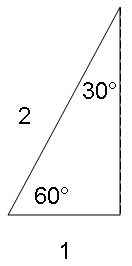
Now at least I had one angle at my beck and call. What about the opposite condition, at sixty degrees?
Turning that angle over doesn’t give you much a visual clue. Pythagoreas, that famous Greek guy, gave us a2 + b2 = c2 for just this situation, where c is the hypotenuse. Solving for one of the legs:
a2 + b2 = c2
a2 + (1)2 = (2)2
a2 + 1 = 4
a2 = 4 - 1
a2 = 3
a = √3
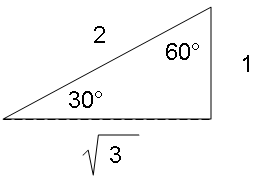
So if the wind is 2, the crosswind is √3; or the crosswind is equal to √3 / 2. It doesn’t actually roll off the tongue, now does it? Pulling up a calculator we find √3 / 2 = 0.87 which is a pretty high ratio, almost 90 percent. That would have to do:

A sixty degree crosswind is equal to ninety percent of the full wind factor.
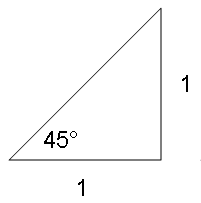
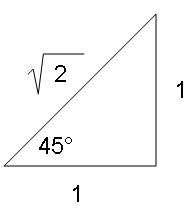
Now, what about 45 degrees? Back to the drawing board:
It looked like another job for Pythagoreas:
a2 + b2 = c2
(1)2 + (1)2 = c2
1 + 1 = c2
2 = c2
c = √2
So a 45 degree crosswind becomes the wind divided by the square root of 2. The mighty calculator converts 1 / √2 into 0.71, about 3/4-ths:

A forty-five degree crosswind is equal to three-fourths the full wind factor.
The forty-eight weeks of undergraduate pilot training, we were told, was like trying to take a drink from a fire hose. There was a lot to take in and the human brain can only absorb so much. I kept that plastic tab on my crosswind chart and used it. As the years went on, however, I relied more on the rules than the chart. It was becoming apparent these rules could be life saving.
Postscript
Thirty years later, flying a Gulfstream V, we were turning base to runway 26 at Maun, Botswana. We knew it was windy because of the dust blowing on the surface and the uncomfortable ride we were getting from 1,500 feet above. The GV has a crosswind limit of 28 knots but tower didn’t seem understand our “Say winds” request. Finally, on short final tower called the winds for us: 300 degrees at 35 knots. The other pilot started to reach for the chart in his checklist and flipped to the wrong page. After a few of his expletives I said, “Relax, the crosswind is less than 27 knots, we’re okay.” After we landed he finally found his chart.
“Twenty three knots,” he said, “how did you know that?”
“Easy,” I said, “the wind was less than 45 degrees off heading where the crosswind is equal to three-quarters the full value. A quarter of 36 is 9, three-quarters of 36 is 27, so we know the wind has to be less than that because the angle is less. The wind at 45 degrees is three-quarters the full value. You should commit that to memory.”
“No,” he said as if talking about a genetic disorder or amputated limb, “I can’t do math.”