I don't remember the last time I saw a penetration — a high altitude arrival procedural with a steep descent gradient — and I venture to say few pilots would even recognize one. For that matter, I can't think of a current day application, other than perhaps military combat ops. But this was important enough for me to think about it way back when so I am keeping it in my notes, because . . . If You Have to Make it Hard, at Least Make it Simple (1980)
— James Albright
Updated:
2020-01-10
By the time I got to it, the Strategic Air Command was over thirty years old. They started flying when the only criteria was getting the bombs over the north pole and even those who flew the tanker learned to do things one way and one way only: the SAC way.
By 1980, the country had already been through Jimmy Carter and the aviation world was learning to do things more efficiently and with less fuel, because Jet-A gas was so expensive. But in SAC we were still flying high altitude penetrations when going from en route to landing. It was time consuming, fuel costly, and not always the safest way to get from the stratosphere to terra firma. But it was the SAC way.
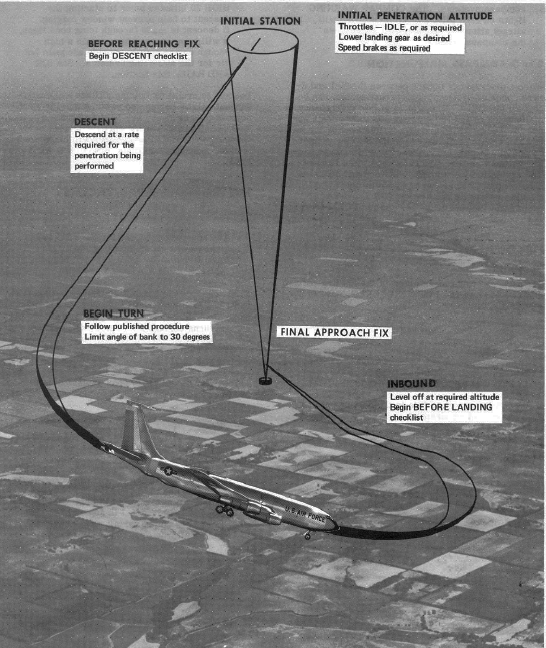
You typically flew over the field, threw out the anchor, and proceeded outbound on a specified radial. At a specified altitude, or half the distance to the ground if not specified, you turned with 30 degrees of bank and intercepted an inbound radial. If your descent rate was what the approach designers envisioned, you would roll out on course and all was well. If not? Well, things got complicated. The bank angle was another issue. Using 30 degrees usually meant you rolled out too early and a slow intercept meant less time on course down low, where it really counted.
My mantra, even back then, was “learn to do it the way the pros do it. If that doesn’t work, adjust.” After three months of copilot school and six months operational, it was clear to me that the pros didn’t know what they were doing. It was time to adjust.
The high altitude approaches that used set courses and arcs were easy enough. The ones that bugged me were the “teardrop” penetrations, so called because they involved heading away from a navigation aid and turning a teardrop course inbound. These were the approaches with the least amount of guidance and the most opportunity for screwing things up.
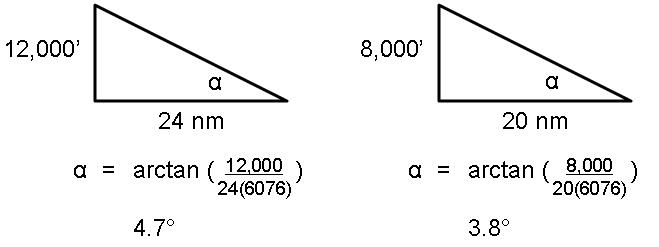
Flipping through our DoD approach plates, I discovered that there was actually a standardization into the construction of high altitude tear drop penetrations. You never had to lose more than 12,000 feet before turning, and if this was the case, your inbound turn would be 18 degrees and you would be required to do this in 24 nautical miles. The gentlest teardrops seemed to require 8,000 feet altitude loss, followed by an inbound turn of 22 degrees within 20 nautical miles. Now I had something to work with!
First off: the descent rate. Mother SAC said we had to make these descents with the landing gear extended and this seemed to work out. With much more than a 3 degree descent, the KC-135A would accelerate without either the landing gear or speed brakes extended. I thought the speed brakes would be better, but the SAC standardization gurus disagreed. Still, it would be nice to verify drag was required. Trigonometry to the rescue:
So in both cases the descent angle exceeded 3 degrees; some kind of drag device was indeed required. It looked like there was a correlation with the descent rate; in that 12,000 divided by 24 is 500 and 8,000 divided by 20 is 400. This looked like a good wag in the making; in fact, it could be generalized to all climbs and descents.

Climb or Descent: Change in altitude divided by change in distance divided by 100 equals the required climb or descent angle.
It wasn’t Einstein, but it was a thing of beauty. It had the added benefit of being useful for the other high altitude penetrations that were not made up of teardrops. Some had varying arc lengths, some were straight lines with bends in them, and some of them were just straight shot, screaming dives. Now I could come up with a descent angle for them all. Learning how much drag was needed, that was for a future project.
Now, on to the bank angle required.
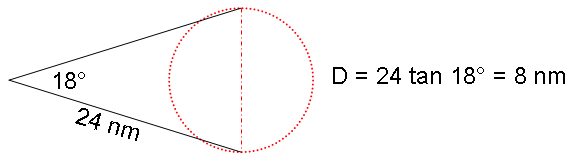
Looking at the approach from above, the so-called “God Angle View,” the most extreme case required flying a radial outbound 24 nautical miles out, turning, and then flying back inbound on a radial which described an 18 degree difference. The distance between those two points was found with simple trigonometry and came to 8 nautical miles.
A quick search of my aero textbooks dug up the formula for the radius of a turn, albeit that radius was given in feet.
Plugging in the tangent of 25 degrees, the conversion from nautical miles per hour (S) to nautical miles per min (V), and the conversion from feet to nautical miles yielded something suspiciously like one of the school rules of thumb:
Solving...
With a little manipulation and conversion, I had a formula for the bank angle required to fly a certain radius in nautical miles, at a certain speed.
We typically flew these things around 200 KIAS so we could extend the landing gear. Our KTAS would be decreasing as we descended so I needed an average number. Converting KIAS to KTAS using my CPU-26, see Properties of the Atmosphere I came up with 270 KTAS to start. Plugging the numbers in I came with a very low bank angle, 8 degrees.
On my next tear drop penetration I used 10 degrees and it worked perfectly. It looked like I had the winning lottery ticked.
I repeated the math exercise for every high altitude teardrop penetration I had ever seen and the answer always seemed to be around 8 degrees. I started using 10 degrees—good round number—and the reaction was either “Hey that’s neat” or “Knock it off, we always use 30 degrees.” I was soon out of the tanker and that kind of dogma was history. The ten degree rule worked well until. . .
Three years later, at the Air Force Instrument Instructor’s School, somebody came up with a better solution:

The required bank angle for a teardrop penetration is the turn radius times 60 divided by the distance between radials in nautical miles.
And that is what I used from that point on, until . . .
Postscript
Six years later, flying the Boeing 747 nobody flew high altitude penetrations, ever. They were too hard on the airplane, they wasted fuel, and they were dangerous. I think the Air Force came to the same conclusion because you don’t see them anymore. Good riddance.