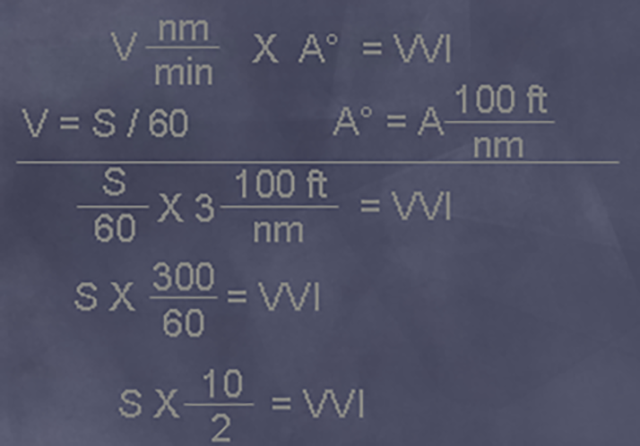According to the gurus of instrument flight in the United States Air Force, the relationship of 60 nautical miles to 1 degree and all the math that follows is fundamental to instrument aviation. When I was first introduced to the concepts, I thought they were brilliant until I had a few years to mull them over and realize they were constructed on faulty math. But it gave us pilots an easy way to figure things out and that was good enough. It was critical back in the days of pure analog cockpits used for instrument flight. These days, I admit, it isn't critical. But having a firm grasp of 60 to 1 can save your hide when all those electrons misbehave.
— James Albright
Updated:
2012-12-17
I am also told what follows, as I wrote it nearly thirty years ago, is too hard to follow and that my story, TLAR explains the concept more clearly. I suppose we all start flying taught by proponents of "That Looks About Right," and that is a better place to start this story. I'll let you decide, so here goes. . .

The math
Sort of
The Air Force Instrument Instructor Course was an on again off again institution designed to teach a small cadre of instructor pilots the finer points of instrument flying. These select few would then in turn go back to their bases and spread the gospel instrument flying by the numbers.
The school went away for a few years but then after a spate of high profile accidents, the Air Force decided it had to come back. It was several weeks talking math, instrument flying, and pilot techniques. It was great fun.
I showed up with six years of very good instrument flying in my logbook and a notebook filled with my own list of math-based piloting techniques. I showed up with a hope for some way to tie it all together. On day one, I got my wish.
“If anyone can explain this to me right now,” the instructor said, “I will give you credit for the course and you can go home today.”
The class was filled with about twenty pilots, all Air Force captains and all, except me, were what the Air Force called “senior pilots,” pilots with seven years in a cockpit. I was still two years shy of the star on my wings.
Nobody else ventured an answer so I thought why not? “Sixty times the sine of 1 degree equals 1. Give or take.”
“You know that for a fact?” the instructor asked.
“No,” I admitted, “it’s just a guess.”
“Well no credit for guesses,” the instructor said, “but it was a damned good guess. You are right.” There was some snickering from the back of the class, answering my “why not?” question. The instructor went on to explain the unifying theory for all aviation mathematics. If Einstein were a pilot, he would have approved.
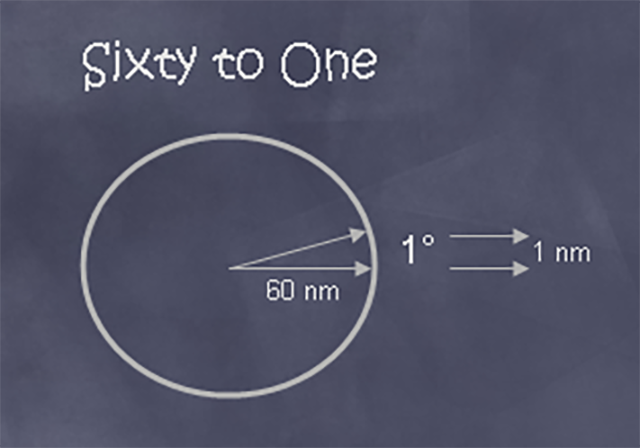
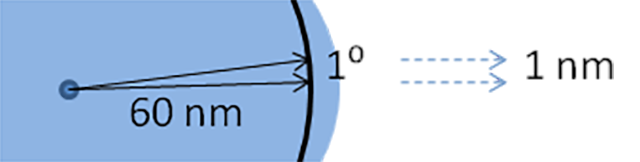
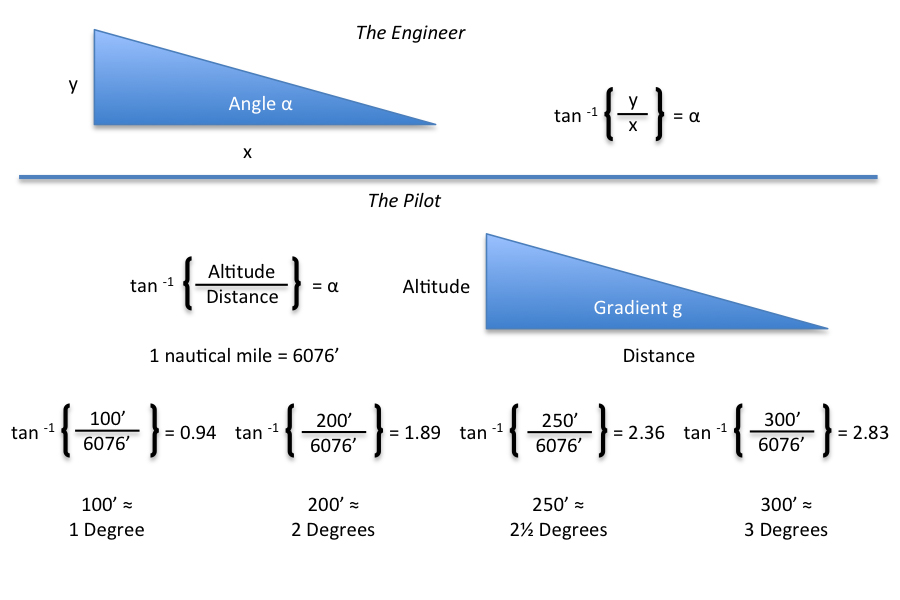
The distance of an arc along a circle is equal to the sine of the angle describing the arc times the radius of the arc. In the case of our 60 nm arc:
Arc Distance = 60 nm x sin ( 1° ) = 1.047144 nm
“If an engineer is looking for the answer one and gets the answer one point oh four seven one four four, what does he call that?” The instructor was looking right at me.
I prefer to remain in the woodwork in these classes, but I had already violated that rule. “Deviation,” I said.
“And what does a pilot call it?” The instructor was now looking to the rest of the class, which was keeping quiet.
“A real pilot calls it bullshit,” the instructor answered his own question. “Can you read zero point oh four seven one four four on any instrument? Of course not. If your calculations are off by zero point oh four seven one four four do you give a shit?” There was some laughter. “Of course not. For the purposes of our math, it’s close enough! Is that okay with you mister engineer?” He was looking at me. I nodded meekly, reminding myself to never again be the first to answer in class. “Good,” the instructor said, “so that’s step one in our path to sixty-to-one nirvana. Let’s take the next step, my young grasshoppers.”
With a quick swipe of an eraser and some chalk, we had a new board to look at.
This one I couldn’t explain and fortunately the instructor had tired of making sport of me in front of the class. (He actually bought me a beer that night at the bar, saying I was the first student to ever answer his opening question correctly.) His explanation was arithmetic genius.
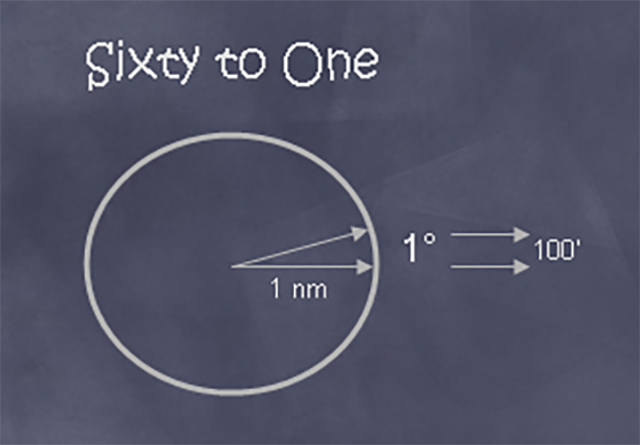
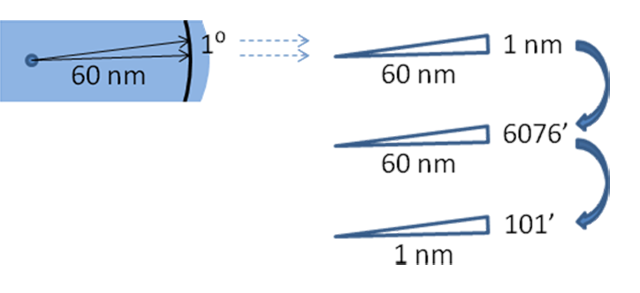
We had already seen proof that 1 degree of a 60 nautical mile arc comes to 1 nautical mile. And we all knew a nautical mile equals 6,076 feet. It was just simple multiplication and division.
“Let’s call it 100 feet,” he said, “because 1 foot is . . .”
“Bull shit!” most of the class said, finishing his statement.
“Good,” he said, “and a 100 feet equals a flight level.”
“Here it is boys and girls,” he said to our all male class, “the crux of this class, the foundation of everything you will ever do as an instrument pilot. If it was up to me, we would tattoo these words on every pilot’s forehead in reverse, so he would wake up every morning and have to stare at them in the mirror while shaving. The smarter among you will realize that means you should be writing this down."

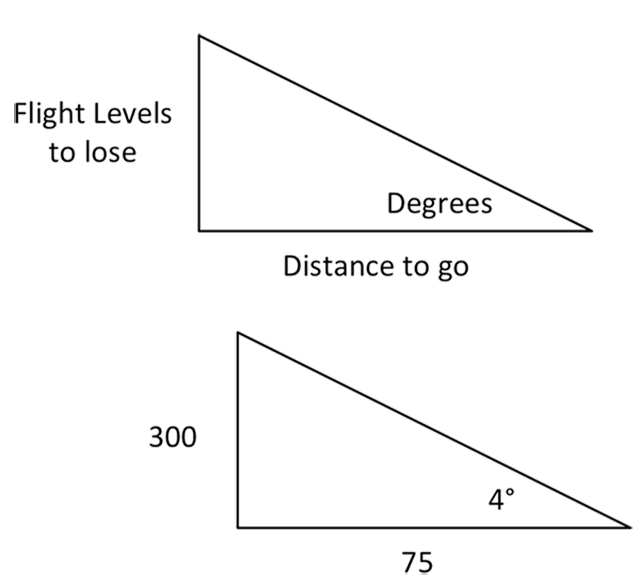
Flight levels divided by nautical miles equals gradient.
Side Bar: Purists and mathematicians are going to protest at this point, "How does that in any way equal gradient? Pilots will accept it and move on; there is so much in our business that is just PFM, pure magic, that we are used to this. But the engineer in me held on to the point and later figured it out. See 60 to 1; Engineer to Pilot Translation for the explanation.
He gave us example after example and I raced to keep up with my pocket calculator doing the math the old fashion way, with trigonometry. It all worked brilliantly.
Let’s say you are at 35,000 feet, 100 miles out and must level off at 5,000 feet by 25 miles. You have to lose 300 flight levels in 75 miles, 300/75 = 4 degrees.
We did a lot of mental math and, as every engineer knows, you can’t do real world math without including the units. We stopped talking about velocity and either spoke of “nautical miles per hour,” “nautical miles per minute,” or whatever the situation dictated.
“Wouldn’t it be a handy thing to know,” a new instructor asked, “exactly what VVI you want when descending on a non-precision approach?”
This was precisely what I wanted. My efforts to date produced pages on pages of tables, one for each approach we flew. Nothing I did was worthy of mental math. I had tried, but more times than not I would confuse myself and revert to “dive and drive” rather than underestimate the descent needed.
“Well feast your eyes on this,” he said, looking straight at me.
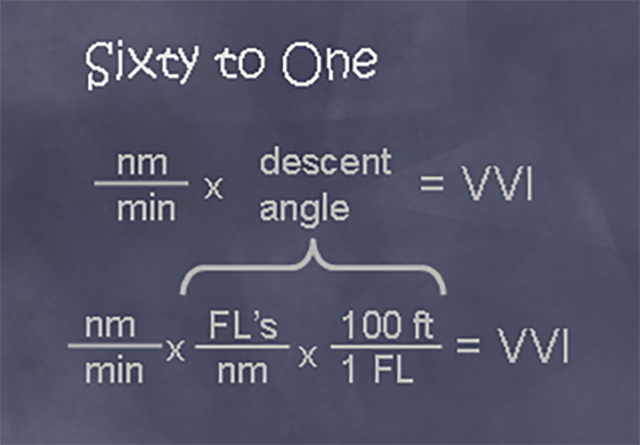
It was, to over use the word of the class, brilliant. We had already proven that descent angle is equal to flight levels to lose divided by nautical miles to lose them. Multiplying by 100 ft divide by 1 flight level was the same as multiplying by one; it just made the units agree. So here, at long last, was an easy way to figure vertical velocity on a non-precision approach.

Nautical miles per minute times descent angle times 100 gives vertical velocity in feet per minute.
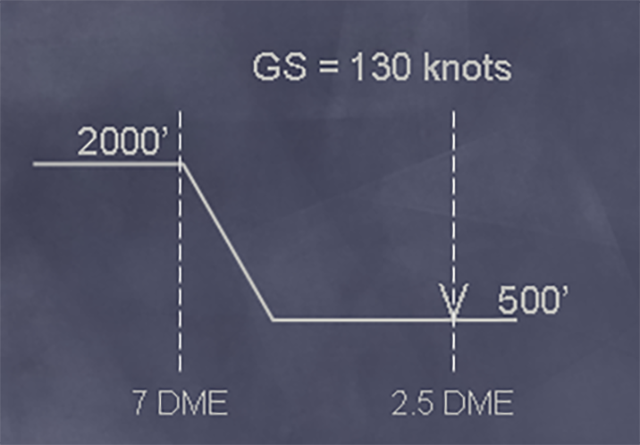
His example looked more complicated than it was at first, none of the numbers were easily computed mentally. But the school mantra, “close enough,” would help.
The altitude to lose was 2000 - 500 = 1500 feet, or 15 flight levels
The distance to lose it was 7 - 2.5 = 4.5 nautical miles
Therefore, the descent angle was 15 / 4.5 = ?
“Well if it were 5 miles that would be easy,” he said, “it would be 3 degrees, right? But we don’t have that kind of distance we have less, so the angle is going to be steeper. Let’s call it 4 degrees and agree that it’s better to be steeper and not steep enough.
The ground speed conversion was no less messy: 130 / 60 = 2-1/6 nautical miles per minute. Pretty close to 2 nautical miles per minute. So the target VVI would be:
4 x 2 = 800 feet per minute — a far cry from the 1,500 feet per minute many pilots assume.
What about a target VVI for a precision approach? When flying an ILS or PAR approach, having a target VVI helps start things on the right foot. For years pilots had been dividing their approach speed by two for a target. I knew early on to use ground speed instead and it worked just fine. The school solution was the same, but it was more than just “it always works,” it was “it always works and here’s why.”

Nautical miles per hour times ten divided by two gives a good three degree glide path VVI.
It all worked out. Using the nautical miles per minute times angle equals vertical velocity, we were able to convert V to S by dividing by 60. The descent angle in degrees was equal to the same number times 100 in feet per nautical miles. We had already proven all of that. From there it was a matter of algebra to prove the age old rule. Sixty-to-one worked again.
We learned about thirty formulas in all and I came back to the squadron ready to spread the math is good gospel. Most the pilots were mildly amused when I demonstrated one technique after another but no one gave it a serious try. “Math is hard.”
The older I get, the more I find myself in the "Math is hard" camp. But I still use these formulas because they have often saved my hide.
Postscript
I have to admit that I was completely hooked by the school and applied its lessons whenever I could. It took a few years, however, for me to realize much of what was taught in the school was pseudo-math. The numbers don't work out, but they are certainly "close enough." So, for you mathematicians out there, all of this is a corruption of science. (See 60 to 1; Engineer to Pilot Translation.) But for all you pilots, this stuff remains pure gold.