Our chosen profession often involves navigating thousands of miles in just a few hours, something that was impossible to do without a navigator with a book of tables and a sextant.
— James Albright
Updated:
2014-05-21
Sea going captains relied on the sun and stars for navigation. By measuring the length of day, from the sun's highest point in the sky from one day to the next, the ship's latitude could be judged. Pendulum-based clocks were almost up to the task. Longitude posed a similar problem, but local noon had to be compared to noon at a known location, usually the departure port. Clocks needed to keep accurate time for months to do this. That's where English clock maker John Harrison came in, inventing just such a clock. His first is now at the Royal Observatory in Greenwich.

1
History of lines of latitude and longitude
- Lines of latitude and longitude began crisscrossing our world view in ancient times, at least three centuries before the birth of Christ. By A.D. 150, the cartographer and astronomer Ptolemy had plotted them on the twenty-seven maps of his first world atlas. Also from this landmark volume, Ptolemy listed all the place names in an index, in alphabetical order, with the latitude and longitude of each — as well as he could gauge them from travelers' reports. Ptolemy himself had only an armchair appreciation of the wider world. A common misconception of his day held that anyone living below the Equator would melt into deformity from the horrible heat.
- The Equator marked the zero-degree parallel of latitude for Ptolemy. He did not choose it arbitrarily but took it on higher authority from his predecessors, who had derived it from nature while observing the motions of the heavenly bodies. The sun, moon, and planets pass almost directly overhead at the Equator. Likewise, the Tropic of Cancer and the Tropic of Capricorn, two other famous parallels, assume their positions at the sun's command. They mark the northern and southern boundaries of the sun's apparent motion over the course of the year.
- Ptolemy was free, however, to lay his prime meridian, the zero-degree longitude line, wherever he liked. He chose to run it through the Fortunate Islands (now called the Canary & Madeira Islands) off the northwest coast of Africa. Later map makers moved the prime meridian to the Azores and to the Cape Verde Islands, as well as to Rome, Copenhagen, Jerusalem, St. Petersburg, Pisa, Paris, and Philadelphia, among other places, before it settled down at last in London. As the world turns, any line drawn from pole to pole may serve as well as any other for a starting line of reference. The placement of the prime meridian is a purely political decision.
Source: Sobel, page 2
2
Latitude
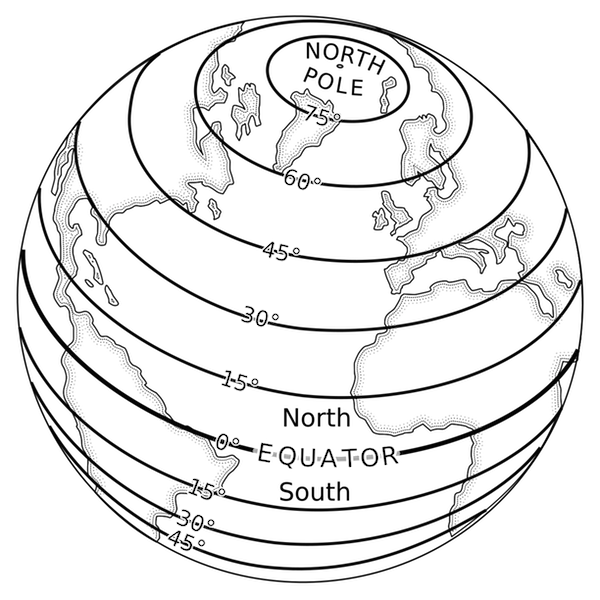
- The zero degree parallel of latitude is fixed by the laws of nature.
- Any sailor worth his salt can gauge his latitude well enough by the length of the day, or by the height of the sun or known guide stars above the horizon. Christopher Columbus followed a straight path across the Atlantic when he "sailed the parallel" on his 1492 journey, and the technique would doubtless have carried him to the Indies had not the Americas intervened.
Source: Sobel, page 2
A good inertial reference system can deduce its latitude by the spinning of the earth and will detect a pilot entry error that disagrees with the sensed motion.
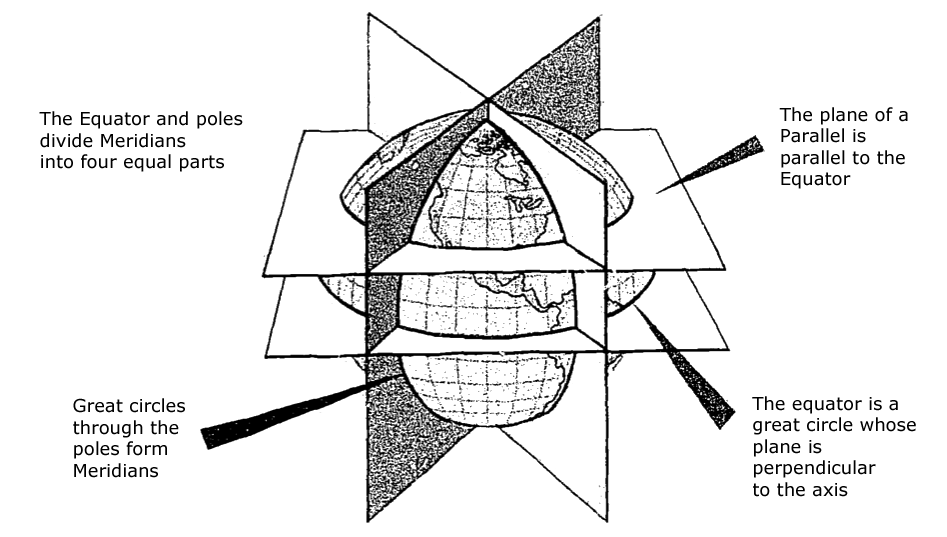
- Once a day, the earth rotates on its north-south axis which is terminated by the two poles. The equator is constructed at the midpoint of this axis at right angles to it. A great circle drawn through the poles is called a meridian, and an infinite number of great circles may be constructed in this manner. Each meridian is divided into four quadrants by the equator and the poles. Since a circle is arbitrarily divided into 360 degrees, each of those quadrants therefore contains 90 degrees.
- Take a point on one of these meridians 30 degrees north of the equator. Through this point pass a plane perpendicular to the north-south axis of rotation. This plane will be parallel to the plane of the equator as shown [in the figure] and will intersect the earth in a small circle called a parallel or parallel of latitude. The particular parallel of latitude chosen is 30° N, and every point on this parallel will be at 30° N. In the same way, other parallels can be constructed at any desired latitude, such as 10 degrees, 40 degrees, etc.
Source: AFM 51-40, page 2-3.
3
Longitude
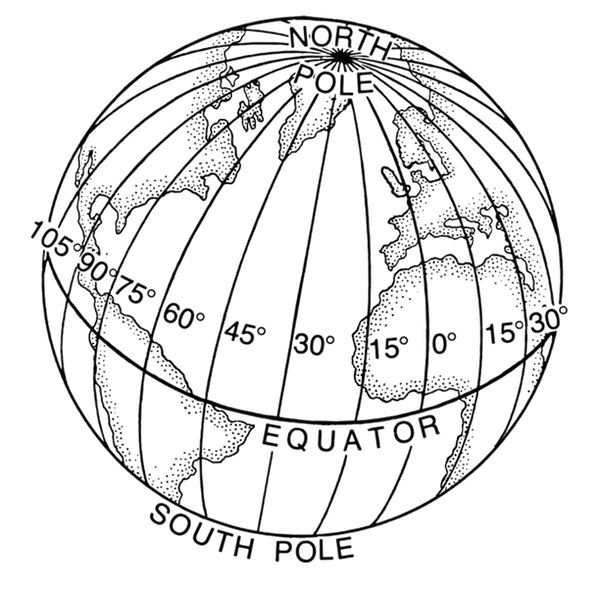
- The zero degree meridian of longitude shifts like the sands of time.
- To learn one's longitude at sea, one needs to know what time it is aboard ship and also the time at the home port or another place of known longitude — at that very same moment. The two clock times enable the navigator to convert the hour difference into a geographical separation. Since the earth takes twenty-four hours to complete one full revolution of three hundred sixty degrees, one hour marks one twenty-fourth of a spin, or fifteen degrees. And so each hour's time difference between the ship and the starting point marks a progress of fifteen degrees of longitude to the east or west. Every day at sea, when the navigator resets his ship's clock to local noon when the sun reaches its highest point in the sky, and then consults the home-port clock, every hour's discrepancy between them translates into another fifteen degrees of longitude.
- Those same fifteen degrees of longitude also correspond to a distance traveled. At the Equator, where the girth of the Earth is greatest, fifteen degrees stretch fully one thousand miles. North or south of that line, however, the mileage value of each degree decreases.
Source: Sobel, page 2
- The latitude of a point can be shown as 20° N or 20° S of the equator, but there is no way of knowing whether one point is east or west or another. This difficulty is resolved by the use of the other component of the coordinate system, longitude, which is the measurement of this east-west distance.
- There is not, as with latitude, a natural starting point for numbering, such as the equator. The solution has been to select an arbitrary starting point. A great many places have been used, but when the English speaking people began to make charts, they chose the meridian through their principal observatory in Greenwich, England, as the origin for counting longitude, and this point has now been accepted by most other countries of the world. This Greenwich meridian is sometimes called the prime or first meridian, though actually it is the zero meridian. Longitude is counted east and west from this meridian, through 180 degrees.
Source: AFM 51-40, page 2-4.
References
(Source material)
Air Force Manual (AFM) 51-40, Air Navigation, Flying Training, 1 July 1973
Sobel, Dava, Longitude: The true story of a long genius who solved the greatest scientific problem of his time, Thomas Allen & Sons Canada Limited, Markham, Ontario, 1995