Trig? Do pilots really need to know trigonometry? No. But much of what we do is governed by it and there are times you wonder about all things navigation, lateral and vertical, where a good dose of trig will explain the unexplainable.
— James Albright
Updated:
2020-05-18
I've added a few practical examples just to show where trig can come in handy.

1
Sum of angles
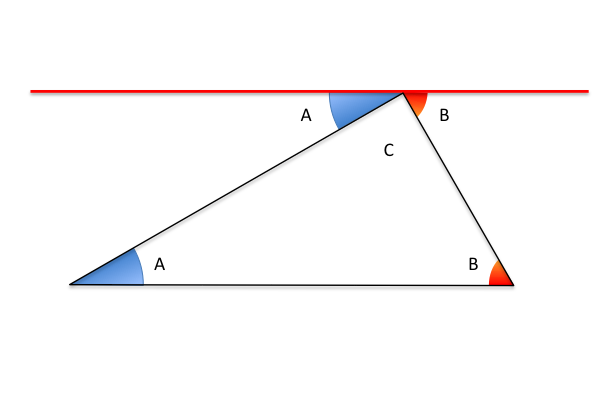
If you draw a triangle with one leg parallel to a straight line, you discover that the angles along the parallel leg are equal to the angles opposite the angle that touches the straight line, which by definition is an angle of 180°. So you can infer that the sum of the three angles in a triangle is 180°.
If you have a right triangle, you know one of the angles is 90°. That means the sum of the other two angles is 90°.
3
Trigonometric functions
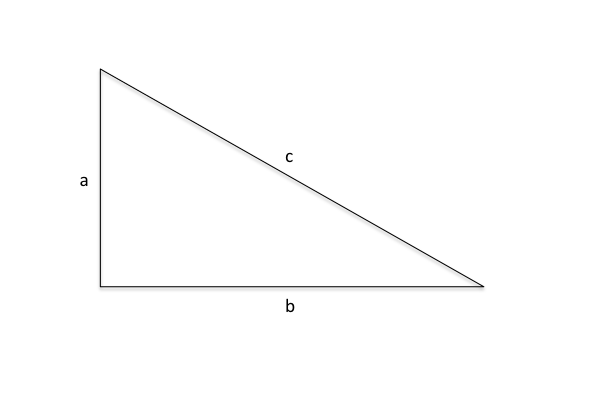
Known: One angle, two sides, Find: Third side
In aviation the triangles are often right angles, which means you will always know at least one of the angles.
Sine
Cosine
Tangent
Cotangent
Secant
Cosecant
Known: One angle and two sides, Find: Second angle
This is handy for determining glide paths. This is known as the "law of sines."
Known: Two sides, Find: Missing angle
4
A few examples
Circling Offset
The sine of 30° = 0.5, which offers us easy math for many situations. When approaching a runway to circle to the opposite side, for example, one often offsets 30 degrees to establish a downwind. The distance offset is equal to half the distance covered in the offset leg. More about this: Circling Approach.
Course Deviation
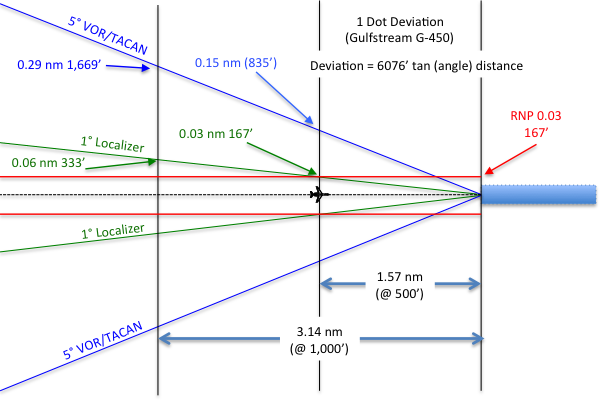
The tangent of an angle provides the relationship of a triangle's two legs adjacent to the right angle. Multiplied by the distance left to travel, the tangent of an angle will provide course deviation. More about this: Stabilized Approach.
Crosswinds
Just as the sine of 30° = 0.5, the cosine of 60° = 0.5. You can also figure that the sine of 60 or the cosine of 30° is √3 / 2 = 0.87, almost 90 percent. The cosine or sine of 45° is 1 / √2 = 0.71, almost three-fourths. That leads to a few handy rules of thumb when it comes to crosswinds:
- A thirty degree crosswind is equal to one-half the full wind factor.
- A forty-five degree crosswind is equal to three-fourths the full wind factor.
- A sixty degree crosswind is equal to ninety percent of the full wind factor.
More about this: Crosswind Landing.
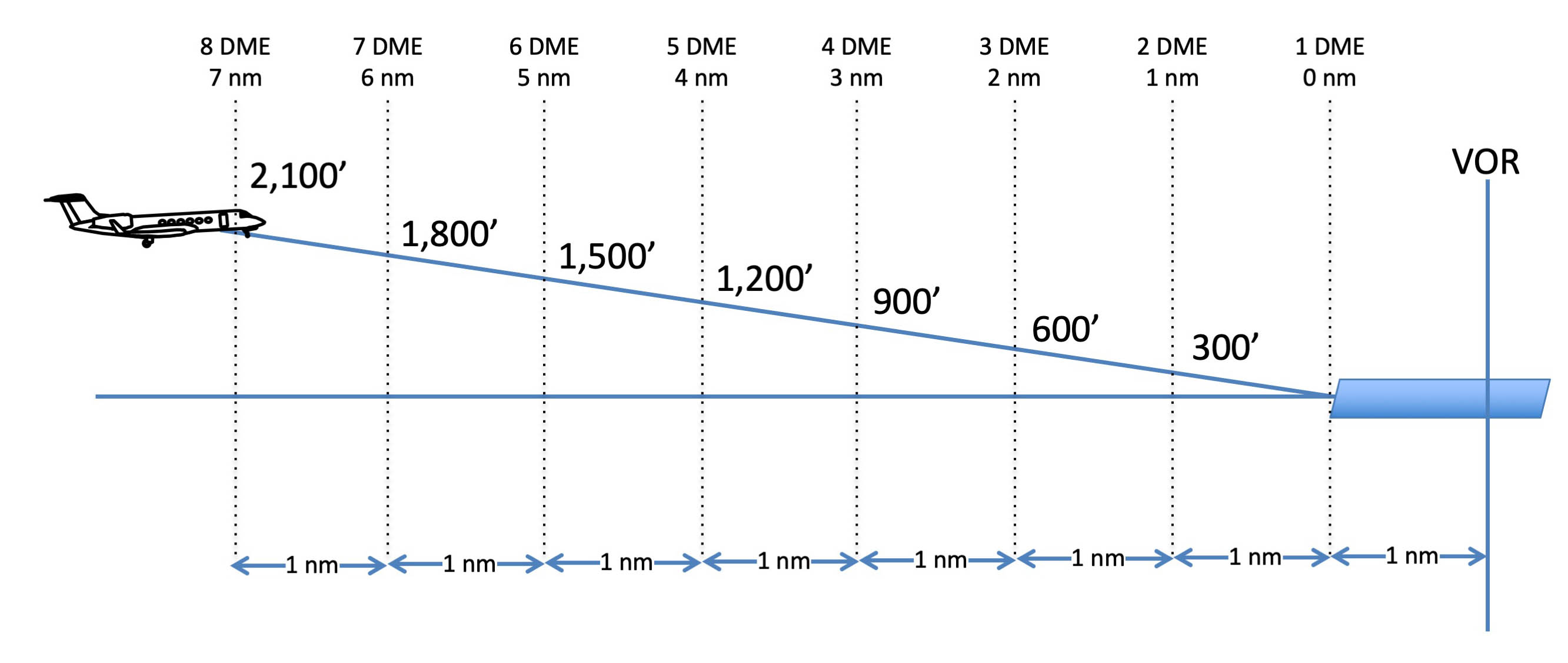
Vertical Navigation on Approach
We often use 300 feet per nautical mile as a wag for how high we should be on final approach. It is pretty close to a three degree glide path, convenient eh?
It is more than convenience, it is trigonometry. The real number, as it turns out, is 318 feet per nautical mile:
5
An example you might not expect
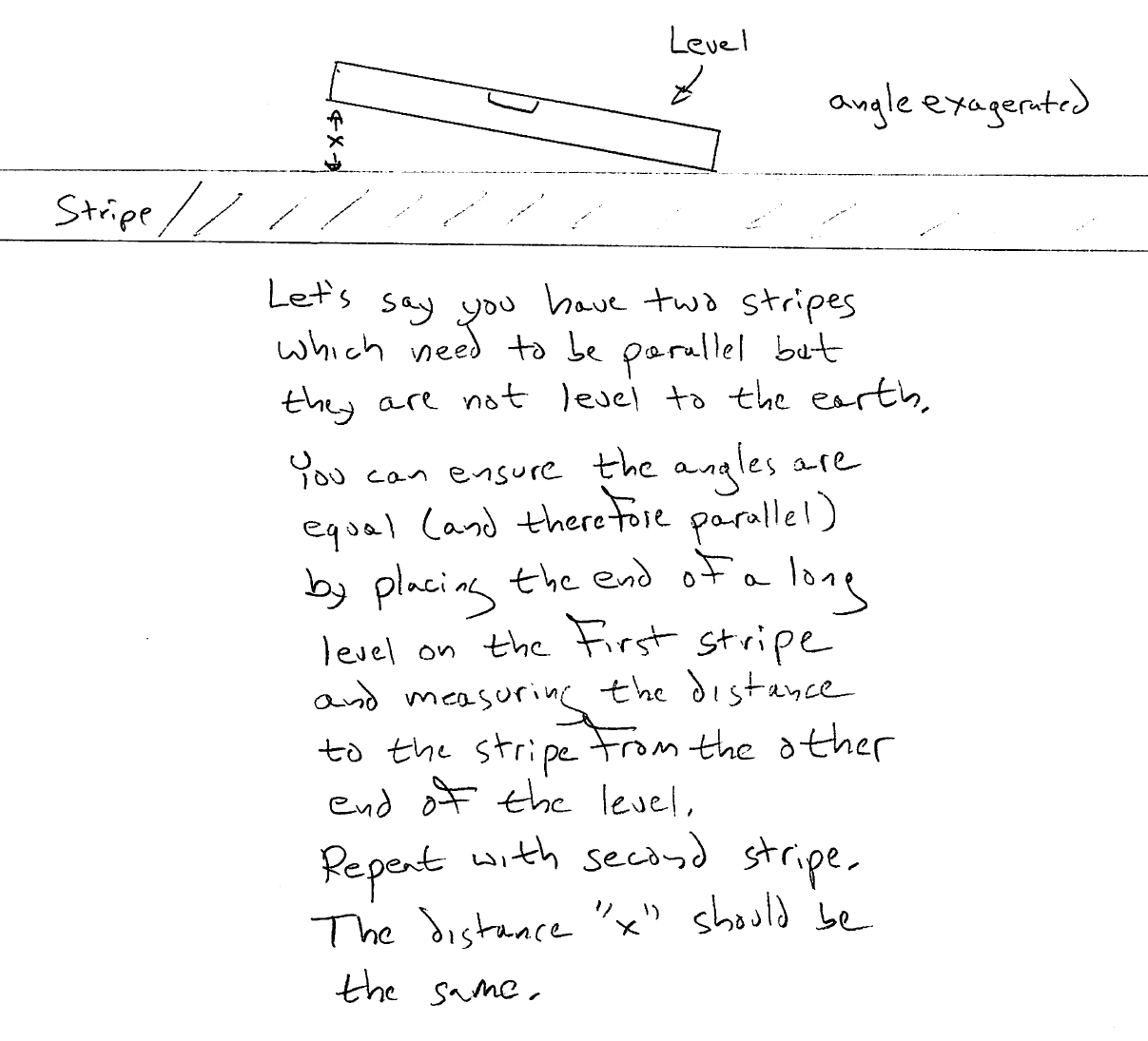
We were about to approve the new paint job on our airplane when one of the designers claimed the stripe on the tail was not parallel with the stripe on the body. The paint specialists assured us they were, since the paint stripes were drawn by a laser. And as everyone knows, lasers are science! Our designer insisted it be checked. The paint specialists said it couldn't be done, since the airplane, as it sat in the paint booth, was not sitting so that any of the stripes could be said to be level to the earth. A simple level wouldn't do us any good. And these specialists were special, it says so right on their title!
We said all they had to do was some trigonometry and they politely implied that trigonometry was not allowed in polite society. They said they would get a jack to lift the nose or main gear to make the body stripes level, but that would take a few hours. While we were at lunch they said they were not allowed to jack the airplane in the paint hangar and if we insisted that the stripes were not parallel, it would delay completion by a week. I drew them some trigonometry without using the term trigonometry:
They said they didn't understand but if we wanted to return they had a level we could use. The body stripe showed a difference of 7 mm from level, the tail was off by 10 mm. They were convinced. They repainted the tail stripe and the next week we repeated the measurement. Here is the level on the body stripe:
Here is the same level on the tail stripe:
At last we were good to go. A week later they discovered their laser was out of calibration. (That's their story and they are sticking to it.)