In the beginning there was TLAR, "That Looks About Right." We pilots learned from experience and tended to fly based on the lessons we had learned over the years. If, for example, pushing the nose over about 1,000 feet prior to level off worked when screaming through the skies with the VVI pegged but waiting till about 300 feet with a slower climb rate was better, well we remembered that.
— James Albright
Updated:
2022-05-30
The problem with TLAR is that is takes experience. If you don't have experience you have to hope the old heads are willing to teach and that you have lots of time to observe. The other problem is that the list of things you had to memorize became very long. When you made a mistake, TLAR became TARA, "That Ain't Right, Adjust."
In the early eighties the United States Air Force had finally had enough of crashing airplanes as a cost of doing business and started getting serious about fixing the mechanical things that were broken and learning how to pass knowledge on from one generation of pilots to the next. The Air Force Instrument Instructor's Course (AFIIC), known over the years under various names, was charged with imparting all that was known about instrument flight.

1
The basis for 60-to-1
Circumference of the earth
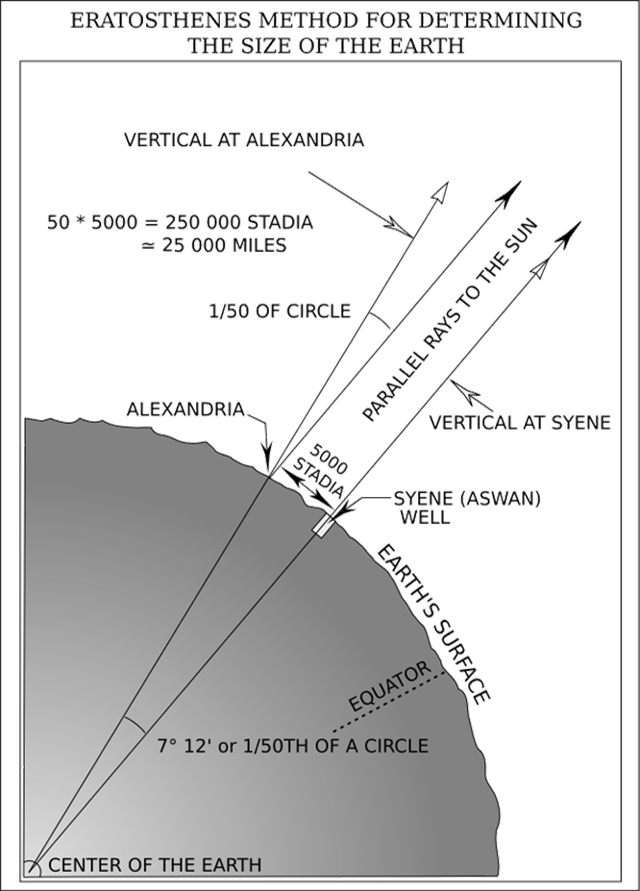
Contrary to common mythology, the idea that the earth is round predates Columbus. An early Greek scholar, Eratosthenes (276 BC - 195 BC) knew that the sun shone to the bottom of a well in the town of Syene (present day Aswan) on the summer solstice, and was therefore directly overhead. And yet it was not directly overhead in Alexandria, just 925 kilometers directly to the north.
Eratostenes realized the sun's rays reach the earth in virtually parallel lines because of its distance. He measured the angle from vertical of the sun's rays in Alexandria when they were vertical in Syene to be 1/50th of a circle. He rationalized that the circumference of the earth would be 50 times the distance between the cities. Remarkably, he was accurate to within 0.4%.
Of course we know the earth is not a perfect sphere, it is wider at the equator than it is north-to-south. We will use 21,654 nm (24,902 statute miles) for the purposes of the computations to come.
360° in a circle
Nobody really knows why there are 360° in a circle, other that a few hypothesis that all sound about right. Ancient astronomers, perhaps, realized each year seems to repeat itself after about 360 days and that the earth, therefore, moved 1/360th of its path around the sun every day.
Latitude
Greek astronomer Claudius Ptolemy wrote about grids that spanned the earth in a treatise he called "Geography." He cataloged places he knew of in relation to the equator (north and south) and the Fortunate Islands (east and west). The system of using degrees north and south for latitude remain with us to this day. The system east and west still exist, of course, though based on a different location. (The Fortunate Islands are now the Canary Islands and Madeira.)
More about this: Latitude and Longitude.
Simple division
The fundamental 60-to-1 theory comes from the following:
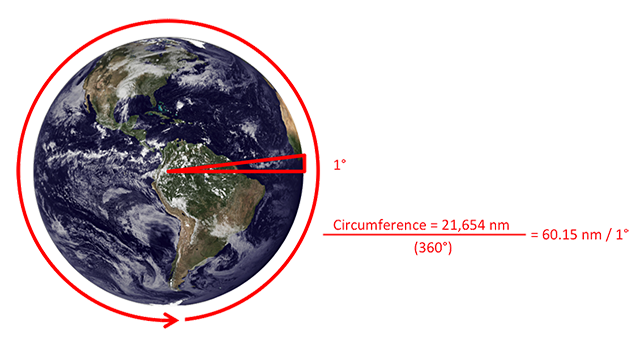
- The earth is round and has a circumference of 21,654 nautical miles.
- Because the earth is round, it can be divided by 360 to produce degrees of latitude.
- 21,654 / 360 = 60.15 nautical miles per degree of latitude.
- A pilot can say 1 degree of latitude equals 60 nautical miles.
Of course this is off by 0.25%. Close enough!
60-to-1, The School Solution
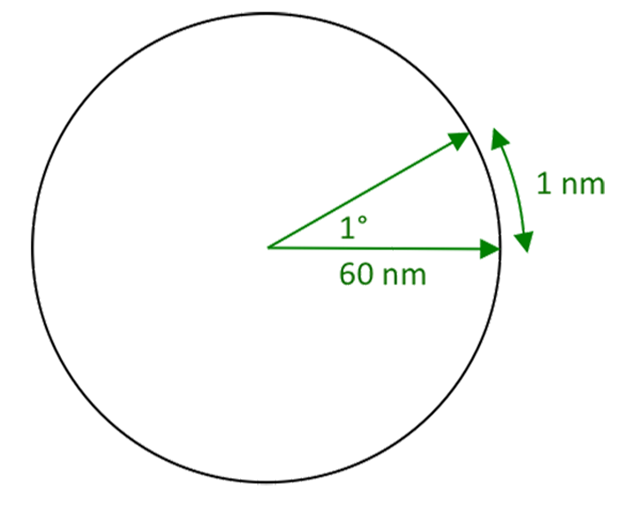
Any international pilot worth the title knows that 1 degree of latitude equals 60 nautical miles, as proven above. From there we come up with the 60-to-1 theory itself.
The theory tells us that 60 nm horizontally becomes 1 nm vertically, at 1°
We also know that 1 nautical mile equals 6,076 feet.
Which leads us to:
If we divide both sides by 60, we aren't changing the equality so the equation remains true:
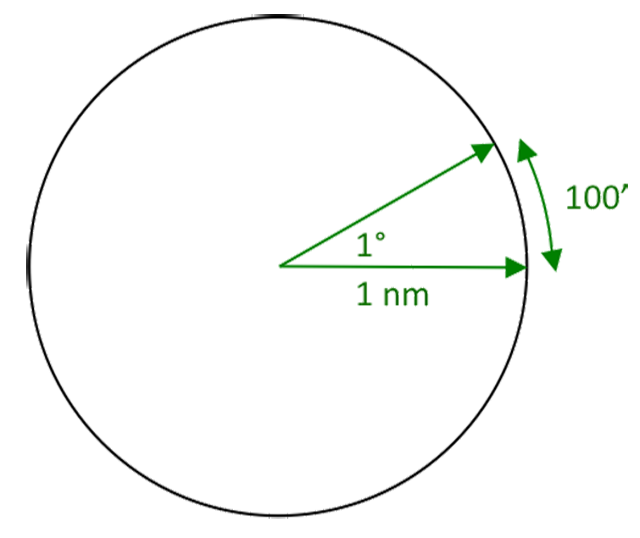
We certainly can't read 1 foot on an altimeter, and certainly not 1.27 feet. So the 60-to-1 vertical flight rule becomes:

It takes 100 feet vertically to climb or descend at a 1° gradient in 1 nautical mile.
It takes 200 feet at 2°, 300 feet at 3°, and so on.
When you are dealing with the distance travelled along an arc, this is certainly true. But other than flying an arc around a point for an instrument approach, airplanes rarely deal with arcs. Most aviation math has more to do with the right triangle . . .
2
Trigonometry
The classic approach to teaching 60-to-1 is to illustrate the division problem shown above and say that is how it works. Don't look at the man behind the curtain! If you want to understand many of the 60-to-1 rules of thumb, however, simple division isn't going to cut it. A little trigonometry is in order. I promise to make this as painless as possible . . .
The Greek word for triangle is "trigonon" and from that we get the study of triangles, trigonometry. It is a subject that makes many pilots wince. In fact, you could argue many pilots became pilots because their high school math classes convinced them they should do something fun for a living, rather than spend their days writing formulas and drawing three angles surrounded by three connected lines. That is unfortunate; much of aviation is based on trigonometry.
When you constrain one of the angles in a triangle to being precisely 90°, a right angle, you can learn a lot about the other parts of the triangle with relative ease. If you draw a circle around the triangle with one point at the center and another at the circumference, the tangent of the circle intersecting the triangle has a few interesting properties.
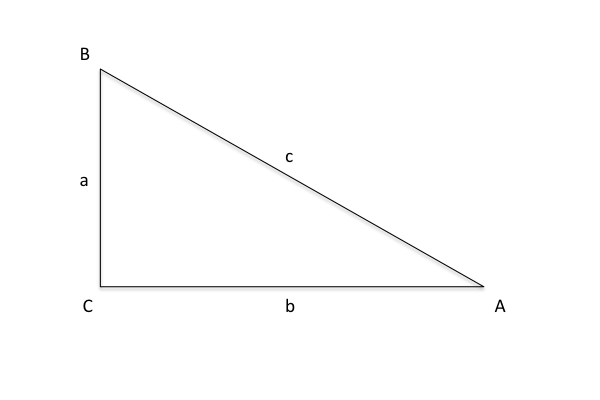
We draw triangles and label the sides with lower case letters. The angle that is opposite that side is labeled by the same letter, in upper case. Just to make things a bit more confusing, we often label the angles using letters of the Greek alphabet, the most common being the letter theta, θ.
The tangent of a triangle is found by dividing the side opposite that angle by the side adjacent to that angle. In a classic mathematical sense, the answer would be presented in radians (of which there are 2π in a circle) but for most uses degrees are preferred.
For example, let's say we have a triangle ABC where a = 1 and b = 2. Using a scientific calculator we see that the tangent of A = 0.1. Now that hardly seems useful, does it?
We can make this function more useful if we could solve for A. This is known as an "inverse function" and the solution for A, in this case, is called the "arc tangent." It can be written as arctangent(A), arctan(A), atan(A), or more properly, tan-1(A).
Our example becomes A = arctan( a / b ) = arctan ( 1 / 2 ) = 27°.
So that is all you really need to know. Just keep in mind this formula converts two sides of a right triangle into an angle. The rest is easy. More about this: Trigonometry for Pilots.
3
Radians
This section is courtesy Al Klayton.
Converting Radians to Degrees and Degrees to Radians
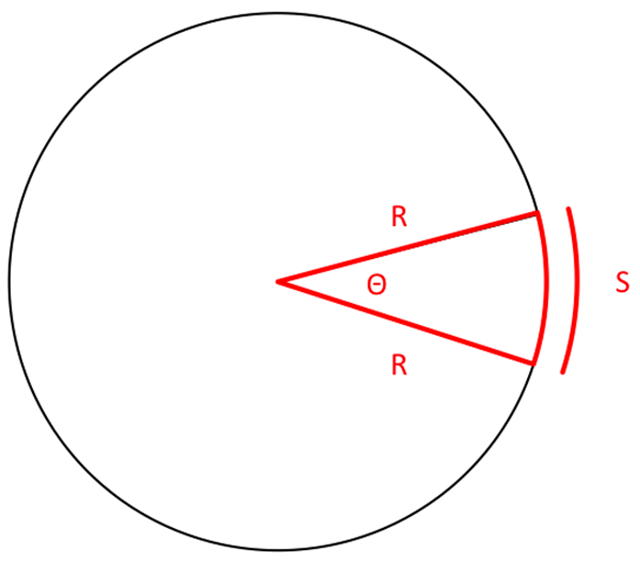
Just like a distance D can be measured in feet D (ft) or nautical miles D (nm), an angle θ can be measured in degrees θ (deg) or radians θ (rad). Like degrees, a radian is defined in relation to the properties of a circle. In particular, an angle θ (rad) is defined as the ratio of the length of a section of the circles’ circumference (arc length S) to the radius R as shown in the figure.
Since we are going to be talking about angles with the Greek symbol theta, θ, with two different units, we will apply a subscript to differentiate between angles measure in radians, θRadians, and degrees, θDegrees.
If the length of S happens to equal R, then
θRadians = S/R = R/R = 1 radian.
If S is twice the length of R, then
θRadians = S/R = 2R/R = 2 radians.
Now if we let S increase to the length of the circle’s circumference then
S = 2πR
and θRadians = S/R = 2πR/R = 2π for a full circle.
So we conclude a complete circle represents 2π radians. But we also know a circle represents 360 degrees. Thus
360 degs = 2π rads
Or 1 deg = 2π/360 rads = π/180 rads, and conversely
1 rad = 360/(2π) = 57.3 degs.
We now can convert back and forth between degrees and radians (like between feet and nm):
and:
Approximating Trigonometric Functions for Small Angles
For small angles it is often useful to approximate that the sine or tangent of the angle θRadians is equal to the angle itself, in radians. In other words, sin(θRadians) = tan(θRadians) = θRadians.
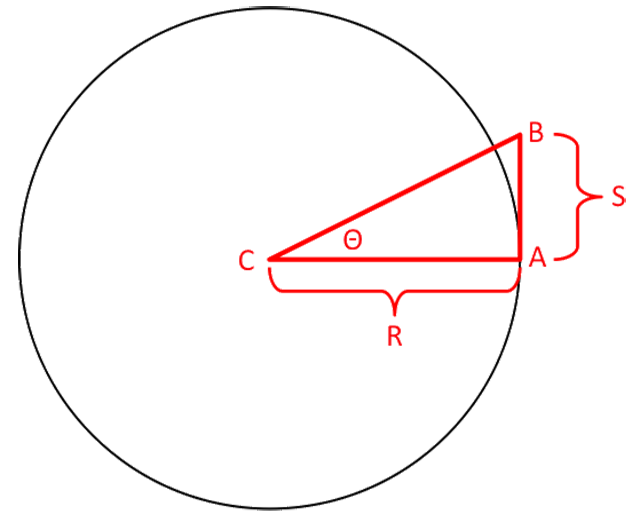
Consider the diagram of the circle and right triangle, which is one way to visualize the small angle approximations Sin(θ) = Tan(θ) = θ in radians. CB and AB represent line segments.
Tan(θ) = AB/R but for small θ we can say AB ≈ S, so we have:
Tan(θ) = S/R and by definition S/R is θ in radians.
Likewise we have:
Sin(θ) = AB/CB but for small angles AB ≈ S and CB ≈ R, so we have:
Sin(θ) = S/R and again S/R is θ in radians. Another conclusion is that for small angles:
Tan(θ) = Sin(θ) although the percent error is a bit different.
Al's conclusion
Al concludes, "There are more mathematically rigorous ways to justify these approximations, but I thought this might provide a little “easy insight”.
4
The rules of thumb, listed
So here you have it, eleven rules of thumb that will help you fly instrument procedures with greater accuracy and less guesswork. You don't need any of the math but I've presented it in the associated links to show there is science behind the art. But keeping a list of the rules of thumb may pay dividends in your operational flying.
Arc distance

The distance traveled along an arc is equal to the arc radius times the arc angle divided by 60.
Why? See: 60-to-1, Engineer-to-pilot Translation / Arc Distance
Bank angle for arc approach

The bank angle required to fly an arc is equal to 30 times the aircraft's turn radius (nm) divided by the arc's radius (nm from the station). At low arc distances, this formula tends to be too high.
Why? See: 60-to-1, Engineer-to-pilot Translation / Arc Around a Point
Circling approach, 90° offset

To provide circling offset when approaching a runway at 90°, overfly the runway and time for 20 seconds (Category D) or 15 seconds (Category C) before turning downwind.
Why? See: 60-to-1, Engineer-to-pilot Translation / Circling Approach from 90° Offset
Circling approach, from opposite runway

To provide circling offset when approaching from the opposite runway, turn 30° away from heading, time for 66 seconds (Category D) or 53 seconds (Category C), and then turn to parallel the runway on downwind.
Why? See: 60-to-1, Engineer-to-pilot Translation / Circling Approach From Opposite Runway
Descent gradient

Flight levels divided by nautical miles equals gradient.
Why? See: 60-to-1, Engineer-to-pilot Translation / Descent Gradient
Descent VVI

Nautical miles per minute times descent angle times 100 gives vertical velocity in feet per minute.
Why? See: 60-to-1, Engineer-to-pilot Translation / Glide Path on Final
Gradient

It takes 100 feet vertically to climb or descend at a 1° gradient in 1 nautical mile.
It takes 200 feet at 2°, 300 feet at 3°, and so on.
Why? See: 60-to-1, Engineer-to-pilot Translation / Descent Gradient
Holding pattern teardrop angle

A holding pattern teardrop angle can be found by subtracting 70 from the airplane's ground speed (in knots) and dividing the result by the holding pattern leg's distance.
Why? See: 60-to-1, Engineer-to-pilot Translation / Holding Pattern Teardrop Angle
Top of descent (3°)

Start descent at three times your altitude to lose in thousands of feet to achieve a three degree gradient.
Why? See: 60-to-1, Engineer-to-pilot Translation / Top of Descent
Top of descent (2.5°)

Start descent at four times your altitude to lose in thousands of feet to achieve a 2.5 degree gradient.
Why? See: 60-to-1, Engineer-to-pilot Translation / Top of Descent
Turn radius

Turn Radius.
Turn radius for a 25° bank angle = (nm/min)2 / 9.
Why? See: 60-to-1, Engineer-to-pilot Translation / Turn Radius
Visual descent point

A Visual Descent Point is found by subtracting the touchdown zone from the Minimum Descent Altitude and dividing the result by 300.
Why? See: 60-to-1, Engineer-to-pilot Translation / Visual Descent Point