False Precision

For example, If your engines have a fuel flow of 1,000 pounds per hour on a gauge that has two digits produced by an LED that change and two painted digits that do not, your accuracy is plus or minus 100 pounds. If the meter reads "1000" the only possible choices above and below are "900" and "1100" because the numbers in the ones and tens place cannot change. Now let's say you have two engines, one indicating 1100 PPH and the other 1200 PPH, so you say you are burning 2,300 pounds per hour. If you have 10,000 pounds of fuel, what is your endurance at this rate? You could say it is (10000 / 2300) = 4.35 hours. Are you willing to bet your life on that? Because of the accuracy of your gages, your actual fuel flow could be as high as (1199 + 1299) = 2,498 PPH. (It might be lower if the gauge pops to the next value at 50 or 51, but we are doing a worst case scenario here.) Now your endurance drops to (10000 / 2498) = 4.0 hours.

Is this important for a pilot? It might be or it might not. But you should understand that rounding errors only get worse as we manipulate them.

1 — A slide rule's precision

2 — The decimal point

3 — Significant digits

4 — Input/output errors

5 — Error propagation

6 — Be accurate, but not too accurate

One of my favorite scenes from the movie “Full Metal Jacket” is where the drill sergeant is telling the recruits that they are married to their rifles and that they must be faithful. At the time they were going through their indoctrination I was going through my own, albeit one that was far less arduous, as a freshman engineering student at Purdue. This was 1974, the war in Vietnam was almost over, and the electronic calculator was still in the future for most of us. But if we had a drill sergeant of sorts in Engineering 101, our credo could have been taken directly from those Marines at Paris Island:

“This is my slide rule.
There are many like it, but this one is mine.
My slide rule is my best friend, it is my life.
I must master it as I must master my life.
Without me, my slide rule is useless.
Without my slide rule, I am useless.”

I paid just over $100 for an ivory slide rule in 1974 because it was required for Purdue University engineering students. I built a four function calculator earlier that year, but those were not allowed in class. I had an abacus from high school, but it wasn't allowed either. Every engineering student that year had to carry a slide rule and a book of tables for doing the things the slide rule could not.

For those of you younger than me but who have been flying for at least twenty years: a slide rule is like your circular E-6B “whiz wheel” designed to solve simple and complex math. For those of you younger than me and who haven’t flown airplanes for more than a decade: a slide rule is three pieces of wood covered in ivory with lines marked at specific intervals so that it could do everything your pocket calculator can do, except for one thing. And that one thing is pretty important. A slide rule doesn’t understand the decimal point.

Let's say you want to multiply thirty times twenty on a slide rule. You do that by placing the left index of the slide over the number 2 of the lower body, the hairline of the cursor over the number 3 of the slide and read the answer 6 under the hairline of the lower body. Simple. Note the numbers 2, 3, and 6. There is no 20 or 30 to choose from. It is up to us to keep all that straight. Is the answer 6, 60, 600? Or maybe 0.6, 0.06, or even 0.006?

So that’s issue one, the decimal point. Math in aviation suffers from three other problems that have vexed engineers since the beginning. The second issue is one of significant digits. We tend to take approximate numbers and turn them into exact numbers. The third issue is that any errors in input turn into errors in output, the so-called “garbage in, garbage out” phenomenon. And finally, the errors add up, sometimes in ways we don't expect. These four problems can give uninformed pilots a false confidence. They will give pilots who know better a reason for extra caution.

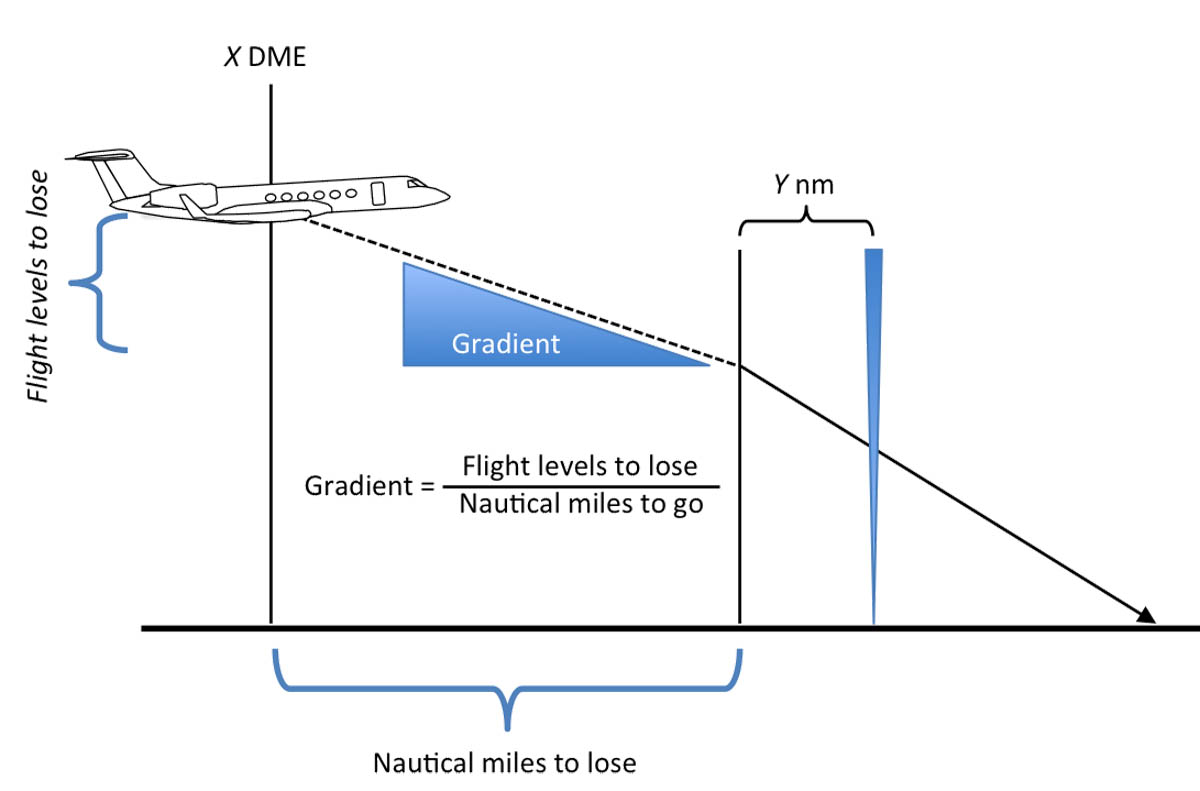
Let’s illustrate the importance of that decimal point in terms any high-altitude airplane pilot can understand. Let's say you are given a step down altitude where you have to be level in a given distance. You may have heard you can divide the altitude to lose by the distance to lose it to get a gradient. This is almost true. Say you are at FL 380 and are told to descend to FL 200 in 60 nautical miles. You need to lose 18,000 feet in 60 miles so the answer is that you need a 300 degree descent gradient! Of course that isn't right, you know it is a 3-degree gradient. You could be more sure of yourself if you memorized the real gradient formula, which is to divide your altitude in hundreds of feet by the distance.

Now let’s move the subject to something we are less comfortable with. Like taxes. Suppose you are making $100,000 per year flying your high-altitude jet in Massachusetts where the state income tax is 5.1% unless you volunteer to give at a higher rate of 5.85%. Your company encourages you to give at the higher rate. What is that going to cost you? Well that should be easy enough for someone who operates an airplane filled with more computing power than existed at the time man first flew to the moon. We want to find out what 0.75% of $100,000 is. It is simple multiplication, after all. So 0.75 times 100,000 is 75 dollars. Or is it 750 dollars? Or maybe 7,500 dollars. No wait, maybe it is 75,000 dollars. Where’s my calculator?

The importance of that decimal point was drilled into us pre-calculator engineering students. We were taught to think of the problem at hand in general terms before going for the exact number. In the income tax example, a 1% tax would have been a penny for every dollar, so 100,000 dollars turns into 100,000 cents, which equals $1,000 dollars. So, we know a 0.75% increase will be less than that, so our answer is $750.

I was once giving a line check to a Global Express crew returning to Hanscom Field, Bedford, Massachusetts (KBED) after a trip from the west coast. We were at 30,000 feet when air traffic control cleared us for descent, with a restriction to cross 100 miles west of Albany, just 20 miles ahead of where we were, at 20,000 feet. It would be the proverbial “slam dunk.” The first officer dutifully programmed the FMS and the captain selected the Vertical Navigation function and said, “let George handle it.” Both pilots went along happily with the discussion at hand while I wondered why we weren’t yet descending. “You need to descend, right now,” I said while trying to figure out what had gone wrong. Looking at the FMS I saw that the first officer had punched in one less zero than required, turning 100 miles into 10, giving us an extra 90 miles for the descent. During the debrief the crew was of course embarrassed but both pilots chalked it up to a “fat finger” input error. I told them that they could have divided the altitude to lose in hundreds of feet by three to come up with what a normal descent point would be. They had to lose 100 hundreds of feet (30,000 – 20,000) and doing that in 100 / 3 = 33 miles would be normal. Doing that in 20 miles would be a slam dunk. They assured me they would do that in the future and I nodded approvingly, knowing they would not.

So the errant decimal point almost got another crew, just as it had got me a few times back at Purdue. But that was only half the problem with our trusty slide rules back then. The other half involved positioning that slat of ivory against a scale and trying to get our target numbers lined up just right. If one hash mark is 0 and the next is 100, where exactly is 75? It is hard to be precise when lining up two lines and a sixteenth of an inch can throw you off by a quarter of the answer.

Significant digits are those that carry meaning to the number in question. There are rules about these things in engineering, but these rules are ignored by most editors for the sake of readability. If you fill your car with gas and the meter finishes at 9.3 gallons, you would never record the result as 9.300 gallons because you know the meter wasn't reporting the number with such precision. If the meter finished at 9.0 gallons, you could say you had "9 gallons" or "nine point zero" gallons. But you would be falsely accurate if you said "nine point zero, zero gallons."

So which digits are significant and which are not? In general:

• All non-zero digits are significant
• Zeros between non-zero digits are significant.
• Leading zeros are never significant.
• In a number with a decimal point, trailing zeros, those to the right of the first non-zero digit, are significant.
• In a number without a decimal point, trailing zeros may or may not be significant. More information through additional graphical symbols or explicit information on errors is needed to clarify the significance of trailing zeros.

A Few Examples

A tour guide at a museum says a dinosaur skeleton is 100,000,005 years old, because an expert told him that it was 100 million years old when he started working there 5 years ago.

A press report in the United States said the following: "European authorities estimated that the bomb used 220 pounds of explosive." Who would estimate such an amount? The European authorities probably estimated the bomb used 100 kg of explosives and the American editor converted the number to pounds. The editor would have been better off saying: "European authorities estimated that the bomb used about 100 kg (220 lbs) of explosives."

Back in the days the 3.5 inch disk was the standard in the computer industry an American could translate these as 88.9 mm disks. But the 3.5 is a rounded number and the disks were actually 90 mm.

Years ago I wanted to capture cockpit audio to go along with video, but I didn't know exactly how to do that. I had a "Y-cord" from my flight examiner days when I needed to tap into the audio from the front two seats but the cockpit in question didn't have a jumpseat with a dedicated interphone panel. So I took the Y-cord and plugged it into my audio recorder. The results were garbled static.

So I took a voltmeter and measured the output of the aircraft's headphone jack and found it was 3.2 volts. I then took a microphone designed for the recorder and found is produced only 0.32 volts, a tenth as much. My recorder's input couldn't handle the aircraft's output.

I remembered a thing called a "step down circuit" from electrical engineering but not how to build it. I saw a Purdue classmate of mine who was an electrical engineer and he drew the circuit for me:

It worked perfectly. For more about my classmate: The Harmon Rule of Error. In fact, his story has a great deal to do with the idea of false precision.

The classic aviator's input/output error involves metric altimetry. I have twice gone into Beijing and got a clearance to 600 meters and saw the pilot in the right seat dial in 600 (the input) into the autopilot's altitude select (ASEL). In that aircraft the ASEL only understood feet, so the 600 translated to 600 feet (the output). The correct procedure was to set the ASEL either through a book of tables or by reference the Pilot's Flight Display (PFD), which did understand meters. Dialing 600 meters in the PFD (input) resulted in a proper ASEL of 2000 (output). This error would have put us 1,400' too low. More about this: Metric Altimetry.

"Errors add up," we often hear. Yes they do, but not always exactly as you might expect. The engineering idea of error propagation is that the result of compound errors is usually the worst case scenario, and that isn't always error addition. Let's look at a few ways to do this:

• Addition. Let's say you have two fuel tanks each with a gauge that is accurate +/- 1,000 lbs. So how sure can you be that you have 10,000 lbs of fuel if the left reads 5,000 and the right reads 5,000? Can you reasonably assume you will have 10,000 lbs +/- 1,000 lbs? No, not really. Each tank could be anywhere from 4,000 to 6,000 lbs, for a total of 8,000 to 12,000 lbs. The error rate of each tank have combined.
• Subtraction. Now let's say we fueled our aircraft for a long trip and the total fuel gauge says we have 28,000 lbs of fuel, plus or minus 2,000 lbs. The trip cancels and the FBO defuels us, saying the truck has an accuracy of 5 percent of whatever fuel it says it has taken from us. We ask to have 10,000 lbs of fuel pumped out of our tanks. Our +/- 2,000 lbs. total fuel will be reduced by an amount +/- 500 lbs. Can we simply add the two error rates and figure on a possible 2,500 lbs variation? No. We will end up with anywhere from 30,000 - 9,500 = 20,500 lbs to 26,000 - 10,500 = 15,500 lbs of fuel, a variation of 5,000 lbs. We have to add all the possible errors, taking the absolute value of the negative errors.
• Multiplication. Finally, let's consider fueling the aircraft somewhere we wanted pounds of fuel, we're used to ordering gallons, but the local fuel truck only understood liters. Many of us take the number of needed pounds, lop off the right zero and add half again as much. So if we wanted 20,000 lbs. of fuel, we would order "20,000 becomes 2,000 add half that for 3.,000 gallons of fuel." (The math would be to multiply the pounds by 0.15) That usually works, it is a ratio of 6.67 pounds per gallon. But it can be off depending on fuel density and temperature. In some parts of the world it can be as low as 6.0 pounds per gallon, an error of 11 percent. Now what about gallons to liters? I know some pilots say it is 3.8 liters to the gallon. The correct answer is 3.785 liters to the gallon, which means the 3.8 pilots are off by 0.4 percent. So is the error rate 11.4 percent? If you wanted 5,000 lbs of that low density fuel added and asked for (5,000 x .15) = 750 gallons times 3.8 for 2,850 liters, you might expect to be off by (2850 x 0.114) = 325 liters. But the 5,000 lbs of fuel actually comes to (5000 / 6.0) = 833 gallons at the lower density and that equates to (833 x 3.785) = 3,154 liters. You will have asked for (3,154 - 2,850) = 304 liters less than you wanted. The error rate is indeed 11.4 percent, error rates in multiplication are the sum of the relative errors.

Sometime before 1983, Air Canada decided it would go metric, though most of its aircraft and crews were brought up in the Imperial world. That year they took delivery of Boeing 767s where the gages read in kilograms instead of pounds and they ordered their fuel in liters instead of gallons. On July 23, 1983 the ground and aircrew of Air Canada 143 made multiple errors that resulted in the aircraft being loaded with half as much gas as it needed, turning it into a "156-tonne glider." More about this: Air Canada 143.

A Poem and a Critique

Thou shalt not be saved by works;
Thou hast been a sinner too;
Ruin'd trunks on wither'd forks, Empty scarecrows, I and you!

Fill the cup, and fill the can;
Have a rouse before the morn;
Every moment dies a man,
Every moment one is born.

—Alfred, Lord Tennyson

In your otherwise beautiful poem, one verse reads, "Every minute dies a man, Every minute one is born"; I need hardly point out to you that this calculation would tend to keep the sum total of the world's population in a state of perpetual equipoise, whereas it is a well-known fact that the said sum total is constantly on the increase. I would therefore take the liberty of suggesting that in the next edition of your excellent poem the erroneous calculation to which I refer should be corrected as follows: "Every moment dies a man, And one and a sixteenth is born." I may add that the exact figures are 1.067, but something must, of course, be conceded to the laws of metre."

—Charles Babbage

From The Thrilling Adventures of Lovelace and Babbage, Sydney Padua, 2015

A lesson for us pilots

Always remember that the source of a number must be considered in its accuracy and when that number is manipulated by other numbers, the errors compound. We like to think in even numbers and that usually works to our favor. But always keep in the back of your mind that there is a "plus or minus" on all numbers except things you can count individually. You may have precisely two fuel tanks. But you cannot say with exact precision how much fuel those tanks contain unless they are empty. And the whole purpose of this exercise is to avoid that outcome.

Padua, Sydney, The Thrilling Adventures of Lovelace and Babbage, 2015.